Adversarial training: a security workout for AI models

Introduction

This week, we continue the AI security @ CVPR ’23 series with adversarial training (AT). AT amends the model’s training dataset with examples crafted specifically to bolster the model’s robustness. The classic AT approach to making a certain class more robust is to add adversarially perturbed images of that class to the training data with the correct label. By doing this, we hope that the model learns to ignore perturbations, because it has seen them in the training data. Adversarial training is a cornerstone of adversarial defense, so it is no surprise it received attention at CVPR ’23. We have seen 9 papers on adversarial training at the conference, summarized below.

Proper training takes class

One of the most ancient rules of security, far predating AI and computer security, is that the attacker will most likely strike at the weakest point in the defenses. Why spend a lot of effort and resources to scale high castle walls if the defenders left a service door on the side open? In machine learning and related disciplines, we know for a fact that not all classes are equally “easy” for a model. Some are harder than others, so the model can be perceived as weaker due to the hard classes. It is reasonable to assume the same is true when looking at adversarial robustness: some classes may be more attackable than others. Therefore, it makes sense to look at adversarial training class-wise.

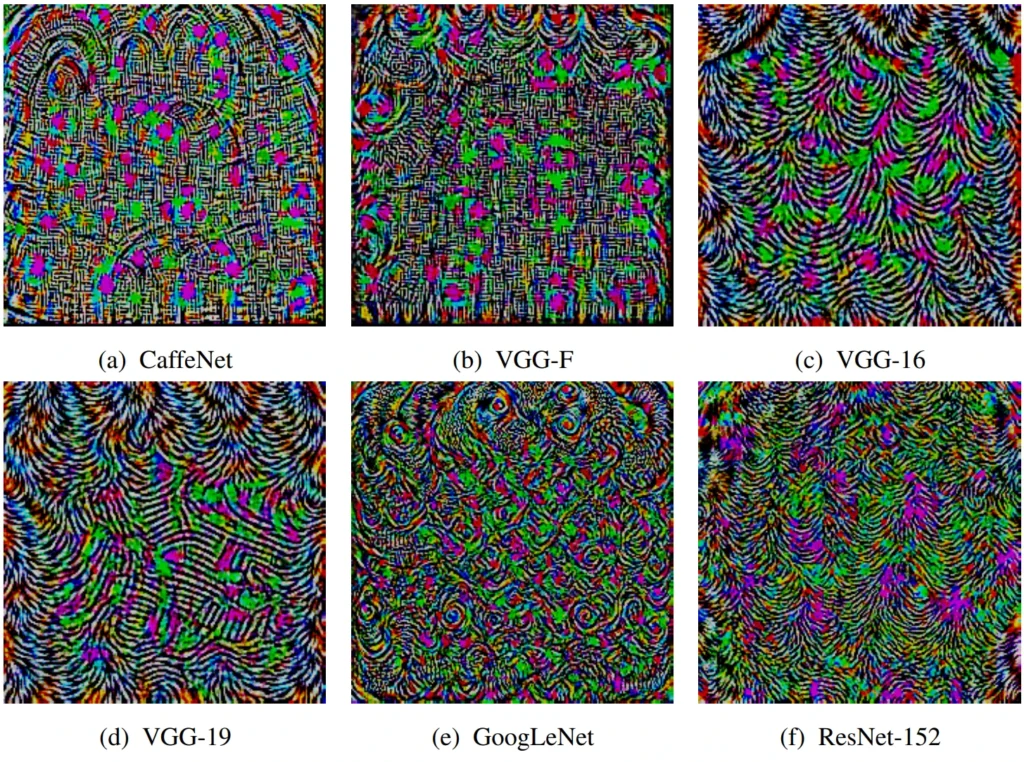
J. Dong et al. present a remarkable idea inspired by universal adversarial perturbations (UAPs), introduced in the seminal CVPR ’17 paper by Moosavi-Dezfooli et al. UAPs are adversarial perturbations that are universal for the given model: adding them to any image will highly likely cause the model to misclassify it. Fig. 1 shows examples of UAPs for various model architectures. J. Dong et al. observe that an adversarial perturbation is essentially a small movement away from the class center across the boundary. By inverting the process and moving in the opposite direction, we move towards the class center, essentially creating a friendly perturbation that helps the classifier. J. Dong et al. move towards a “universal friendly perturbation” by aggregating friendly perturbations of individual instances across classes. Adding these “class-universal friendly perturbations” to the training data compels the model to classify perturbed images closer to the class center. This in turn increases adversarial defense. In my opinion, this paper is quite exciting, presenting a powerful, yet simple idea. Certainly one of my favorites!

Zeming Wei et al. take a deeper look at the weakest classes. A key observation they make is that the least robust class fluctuates across the training epochs. For example, at epoch 24 bird is the weakest class, and at epoch 65 cars are weakest instead. A common adversarial training strategy is to pick the model from the training epoch with the highest overall robustness. That might not be ideal, because it just leaves the class with the lowest robustness in that epoch in the dust. To remedy this, Zeming Wei et al. propose calibrated fair adversarial training (CFA.) CFA adapts the attack configuration for different classes to current class-wise robustness, stabilizing the performance.

Architectural defense in adversarial training

The previous post on robustifying model architectures introduced several key robustness-improving concepts. Two of them, namely randomness and feature analysis, can be used in adversarial training as well.

Jin et al. propose randomized feature training through Taylor expansion. The authors relate (a part of) the trade-off between clean and robust accuracy to loss landscape flatness. In very coarse, but hopefully intuitive terms: a model in training aims to minimize some loss function. The more ragged, “mountainous” the loss landscape is, the harder it is to settle into a minimum. Adversarial and clean training examples are scattered close to one another among the nooks and crannies, and it is hard to train a model that captures both faithfully. This paper shows that randomizing the features flattens the loss terrain, which makes the situation much clearer and organized. This helps the model to capture the nuances of both clean and adversarial examples, closing the gap between the two. In addition, Jin et al. replace the optimization criterion with its Taylor-series expansion as a surrogate, which improves the performance and cuts down on computational time.

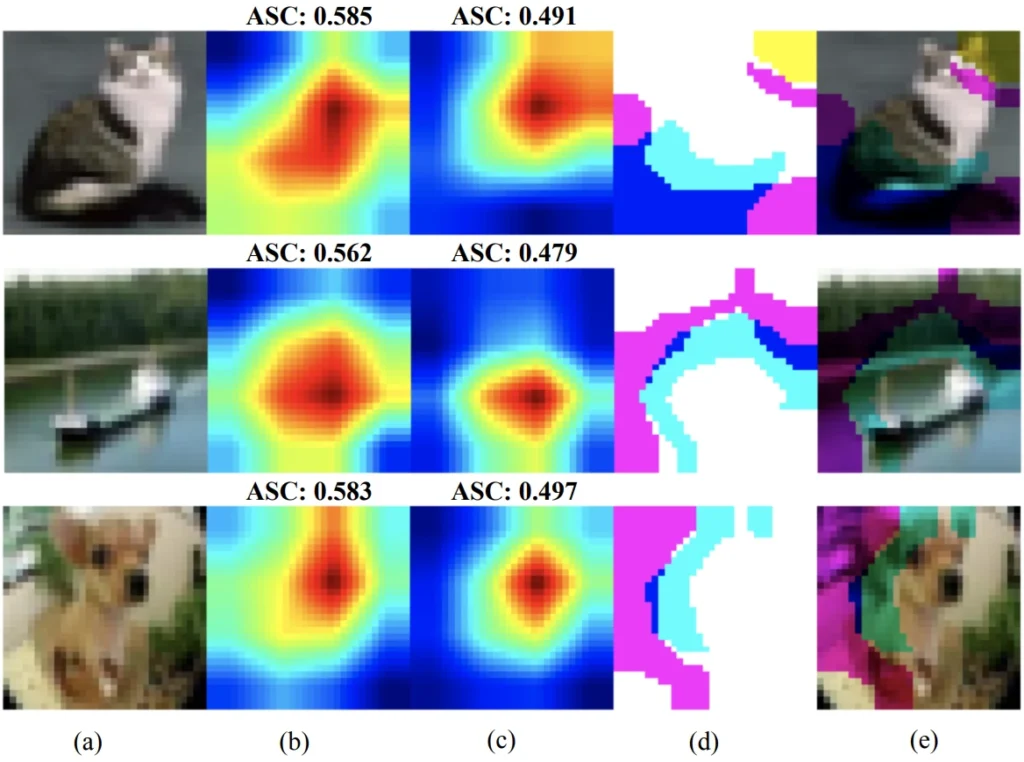
Yin et al. improve adversarial training by incorporating feature analysis. Specifically, they look at the attention intermediate features pay to the regions of a processed image. As we can see in Fig. 2, adversarially-trained features pay attention to specific, smaller regions of the image, whereas non-adversarially trained features look at larger parts of the image. This makes intuitive sense: without adversarial training, the model looks at the entire image to gain as much information it can to make its final decision. After all, we want the model to generalize, i.e., identify the class even with changing environments, poses, lighting etc. An adversarially trained model, on the other hand, has been “scared” into thinking that things may not be the way they seem. The more pixels it looks at, the higher the chance it will be manipulated by an adversarial perturbation. Looking at the minimal evidence of an image belonging to a certain class therefore sounds like a good strategy. But of course, the less it looks, the worse its generalization—and that’s the tradeoff. To combat this, Yin et al. collect stats on the attention span of features on clean data, noting which regions of the image are worth looking at. Using these stats, they then enlarge the attention span of the adversarially trained features. Combining the enlarged attention span and hybridizing features, i.e., mixing clean and adversarially trained ones, leads to improved performance.

Adversarial training with multiple adversaries

Classic adversarial training defends against either a single attack, or a small set of attacks. However, given the great variety of readily-available adversarial attack in existence, it is critically important to be able to defend against multiple attacks at the same time. Hsiung et al. propose general adversarial training (GAT) that aims to defend against composite attacks composed of \(l\)-norm perturbations and manipulations of hue, saturation, brightness, contrast, and rotation. Interestingly enough, the authors use a scheduling algorithm to decide the optimal sequence of attack components. Then, they use component-wise projected gradient descent (PGD) to construct the composite attack. Adding the attacked images to training data is shown to increase performance against multiple attacks at the same time, as illustrated in Fig. 3.

Y. Wang et al.: adopt a game theory approach, casting the problem of attaining multi-attack robustness as cooperative bargaining game (CBG). In a CBG, the players work together towards a common goal, bargaining with each other about splitting the reward gained by completing the joint action. In the adversarial training setting, the players are the adversarial perturbations, and the reward to be split is the adversarial robustness gained by including the adversarial sample(s) featuring said perturbations. The authors observe that a common problem that hampers multi-target robustness is single-player domination. This corresponds to one player (perturbation) taking all the reward, which means the model will be overoptimized to that perturbation and will fail to defend the others. Y. Wang et al. combat this by introducing adaptive budgets: each player has a budget with which to contribute to attacks, and the lower the current defenses against the corresponding perturbation, the higher the player’s budget. This eliminates single-player domination and results in state-of-the-art multi-target robustness.

Robust generalization gap

One of the known theoretical problems with adversarial training is the robust generalization gap: in training, models appear to be more robust than it turns out they really are on the test set. In the CVPR ’23 highlights post, we have seen a highlight paper by Zifan Wang et al. that managed to place an upper bound on the robust generalization error using PAC-Bayesian bound minimization. There are other works that aim to bring the robust training error closer to the robust generalization error, but there is also one paper that throws a curveball of sorts.

Yu & Xu state that model robustness is being overestimated across the board due to floating-point precision errors. According to the authors, gradient-based attacks, which take the lion’s share of all attacks used for adversarial training, suffer from floating-point underflow and rounding errors, which compound and throw the estimate off. To remedy this, Yu & Xu propose a new MIFPE loss (MIFPE = minimizing the impact of floating-point errors), which should lead to more faithful robustness estimates.

List of papers

• J. Dong et al.: The Enemy of My Enemy Is My Friend: Exploring Inverse Adversaries for Improving Adversarial Training
• Hsiung et al.: Towards Compositional Adversarial Robustness: Generalizing Adversarial Training to Composite Semantic Perturbations
• Jin et al.: Randomized Adversarial Training via Taylor Expansion
• Z. Liu et al.: TWINS: A Fine-Tuning Framework for Improved Transferability of Adversarial Robustness and Generalization
• Y. Wang et al.: Cooperation or Competition: Avoiding Player Domination for Multi-Target Robustness via Adaptive Budgets
• Zifan Wang et al.: Improving Robust Generalization by Direct PAC-Bayesian Bound Minimization
• Zeming Wei et al.: CFA: Class-Wise Calibrated Fair Adversarial Training
• Yin et al.: AGAIN: Adversarial Training With Attribution Span Enlargement and Hybrid Feature Fusion
• Yu & Xu: Efficient Loss Function by Minimizing the Detrimental Effect of Floating-Point Errors on Gradient-Based Attacks

Subscribe

Enjoying the blog? Subscribe to receive blog updates, post notifications, and monthly post summaries by e-mail.